Técnicas de Matriz Resposta com Aproximações de Baixa Ordem Aplicadas a Problemas de Transporte de Fótons

Iram Barbaro Rivas Ortiz; Susana Marrero Iglesias; Francisco Bruno Souza Oliveira; Paulo Eduardo Ambrósio; Dany Sanchez Dominguez

doi:10.14295/vetor.v33i2.16440

Authors

Iram Barbaro Rivas Ortiz UESC https://orcid.org/0000-0001-6917-0102
Susana Marrero Iglesias Programa de Pós-Graduação em Modelagem Computacional em Ciência e Tecnologia – Universidade Estadual de Santa Cruz
Francisco Bruno Souza Oliveira Programa de Pós-Graduação em Modelagem Computacional em Ciência e Tecnologia – Universidade Estadual de Santa Cruz https://orcid.org/0000-0002-9847-7290
Paulo Eduardo Ambrósio Programa de Pós-Graduação em Modelagem Computacional em Ciência e Tecnologia – Universidade Estadual de Santa Cruz https://orcid.org/0000-0002-6043-3591
Dany Sanchez Dominguez Programa de Pós-Graduação em Modelagem Computacional em Ciência e Tecnologia – Universidade Estadual de Santa Cruz https://orcid.org/0000-0002-0640-2970

DOI:

https://doi.org/10.14295/vetor.v33i2.16440

Keywords:

Response Matrix Spectral Nodal Methods, Discrete Ordinate Formulation, Radiative Transfer

Abstract

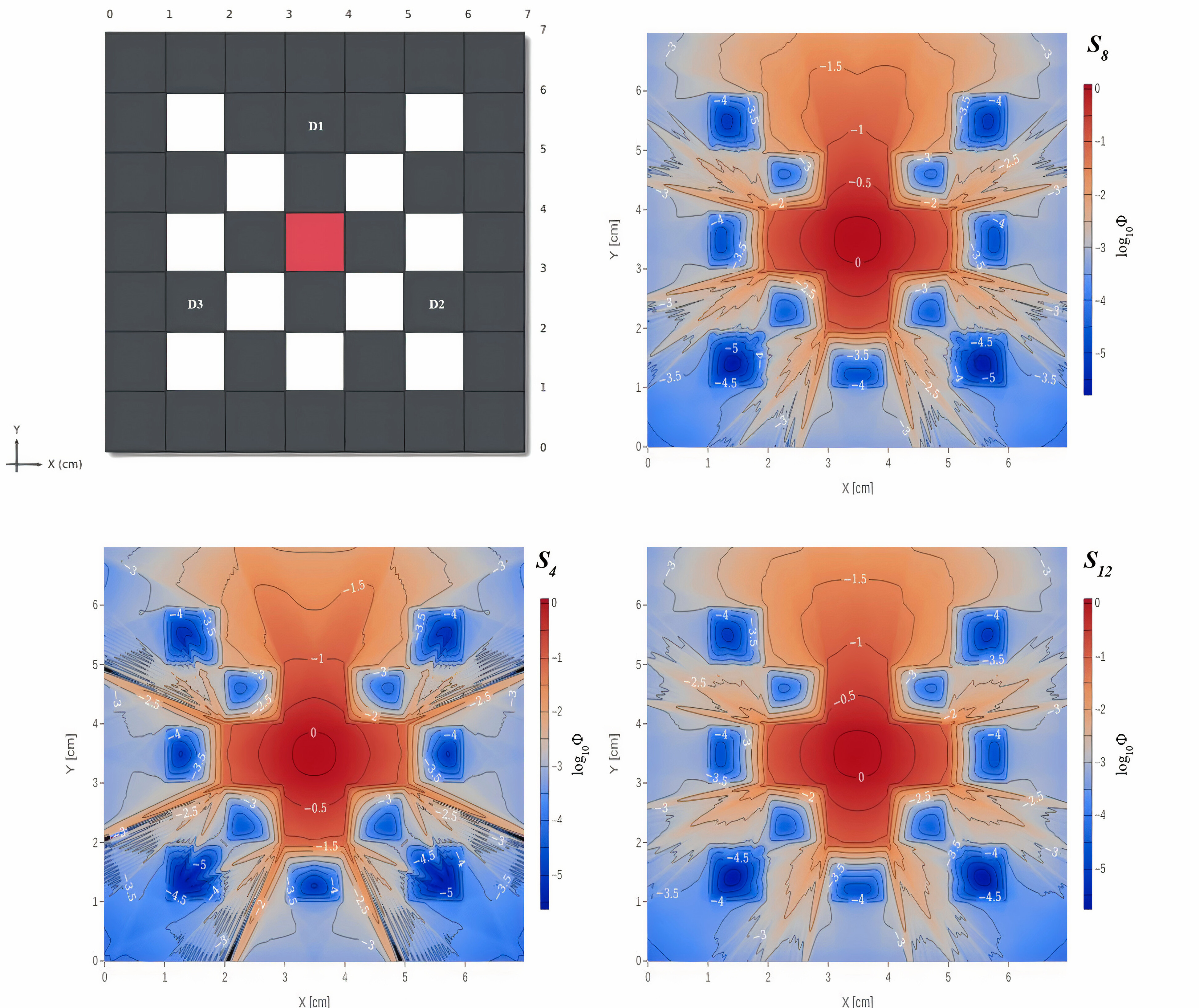
Radiative transfer and photon transport problems are frequently encountered in various fields of science and engineering, ranging from computerized tomography and radiotherapy to astrophysics, non-destructive testing of materials, radiological protection, among other domains. Challenges persist in this field, including the need for more accurate and comprehensive data, the incorporation of more realistic and complex geometries, and the development of efficient algorithms to solve the photon transport equation as a mathematical model. This work introduces approaches that employ response matrix techniques with low-order approximations to address problems related to photon transport. Specifically, the Response Matrix - Nodal Constant (RM-CN) and Response Matrix - Full Linear Nodal (RM-FLN) methods are presented, considering the isotropic phase function in Cartesian two-dimensional geometry, gray atmosphere, and the discrete ordinates (S_N) formulation of the photon transport equation. The performance of the methods is evaluated in terms of accuracy by solving a model problem. Both response matrix methods generate accurate results for coarse spatial discretization grids, with the best results reported by the RM-FLN method. However, the computational cost is higher when compared to the RM-CN method for the same spatial discretization grid. Finally, the discrete ordinates formulation correctly models the wave effects generated between the absorbing regions of the problem, and ray effects are mitigated as the angular order of the formulation increases.

Downloads

Download data is not yet available.

References

O. N. Vassiliev, T. A. Wareing, J. McGhee, G. Failla, M. R. Salehpour, e F. Mourtada, “Validation of a new grid-based Boltzmann equation solver for dose calculation in radiotherapy with photon beams,” Physics in Medicine & Biology, vol. 55, no. 3, pp. 581–598, 2010. Disponível em: https://dx.doi.org/10.1088/0031-9155/55/3/002

J. Nuyts, B. D. Man, J. A. Fessler, W. Zbijewski, e F. J. Beekman, “Modelling the physics in the iterative reconstruction for transmission computed tomography,” Physics in Medicine & Biology, vol. 58, no. 12, pp. R63–R96, 2013. Disponível em: https://dx.doi.org/10.1088/0031-9155/58/12/R63

A. M. Oliva e H. Alves Filho, “Spectral-nodal deterministic methodology for neutron shielding calculations using the X,Y - geometry multigroup transport equation in the discrete ordinates formulation,” VETOR, vol. 31, no. 1, pp. 72–83, 2021. Disponível em: https://doi.org/10.14295/vetor.v31i1.13472

M. C. Betancourt, L. R. Mazaira, C. R. G. Hernández, D. Dominguez, e C. A. B. O. Lira, “Neutronic simulation of the iPWR nuclear core using a SERPENT code,” VETOR, vol. 31, no. 1, pp. 84–93, 2021. Disponível em: https://doi.org/10.14295/vetor.v31i1.13575

E. W. Larsen, G. Thommes, A. Klar, M. Seaid, e T. Gotz, “Simplified PN approximations to the equations of radiative heat transfer and applications,” Journal of Computational Physics, vol. 186, no. 2, pp. 652–675, 2002. Disponível em: https://doi.org/10.1006/jcph.2002.7210

B. D. Rodriguez, M. T. Vilhena, e B. E. Bodmann, “An overview of the boltzmann transport equation solution for neutrons, photons and electrons in cartesian geometry,” Progress in Nuclear Energy, vol. 53, no. 8, pp. 1119–1125, 2011, International Nuclear Atlantic Conference - INAC 2009. Disponível em: https://doi.org/10.1016/j.pnucene.2011.06.009

T. G. McClarren e C. D. Hauck, “Robust and accurate filtered spherical harmonics expansions for radiative transfer,” Journal of Computational Physics, vol. 229, no. 16, pp. 5597–5614, 2010. Disponível em: https://doi.org/10.1016/j.jcp.2010.03.043

A. Buchan, A. Calloo, M. Goffin, S. Dargaville, F. Fang, C. Pain, e I. Navon, “A POD reduced order model for resolving angular direction in neutron/photon transport problems,” Journal of Computational Physics, vol. 296, pp. 138–157, 2015. Disponível em: https://doi.org/10.1016/j.jcp.2015.04.043

N. N. T. Mai, K. Kim, M. Lemaire, T. D. C. Nguyen, W. Lee, e D. Lee, “Analysis of several VERA benchmark problems with the photon transport capability of STREAM,” Nuclear Engineering and Technology, vol. 54, no. 7, pp. 2670–2689, 2022. Disponível em: https://doi.org/10.1016/j.net.2022.02.004

A. Charette, J. Boulanger, e H. K. Kim, “An overview on recent radiation transport algorithm development for optical tomography imaging,” Journal of Quantitative Spectroscopy and Radiative Transfer, vol. 109, no. 17, pp. 2743–2766, 2008. Disponível em: https://doi.org/10.1016/j.jqsrt.2008.06.007

J. J. Duderstadt e W. R. Martin, Transport Theory, 1a ed. New York: John Wiley & Sons, 1978.

S. Chandrasekhar, Radiative Transfer, 1a ed. New York: Dover Publications, Inc., 1960.

E. Lewis e J. Miller, Computational methods of neutron transport equation, 1a ed. New York: John Wiley & Sons, 1984.

R. C. Barros e E. W. Larsen, “A spectral nodal method for one-group X,Y-geometry discrete ordinates problems,” Nuclear Science and Engineering, vol. 111, no. 1, pp. 34–45, 1992. Disponível em: https://doi.org/10.13182/NSE92-A23921

O. P. Silva, M. R. Guida, H. A. Filho, e R. C. Barros, “A response matrix spectral nodal method for energy multigroup X,Y-geometry discrete ordinates problems in non-multiplying media,” Progress in Nuclear Energy, vol. 125, p. 103288, 2020. Disponível em: https://doi.org/10.1016/j.pnucene.2020.103288