Analysis of beams on elastic base via variational methods

Abstract

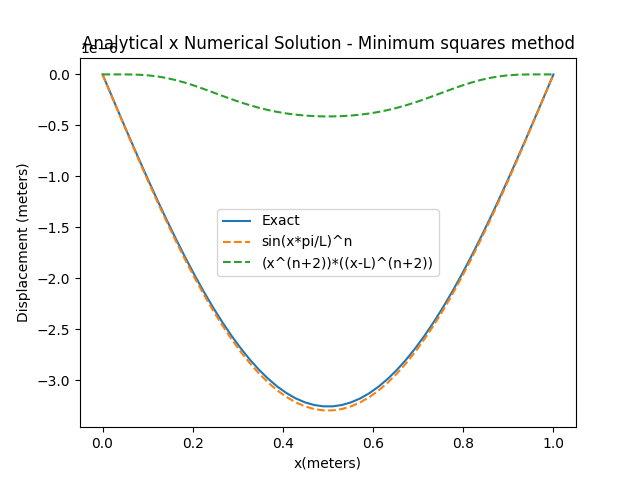
The study of beams is one of the main problems investigated in Civil Engineering, and these structures are governed by differential equations. This article seeks to identify numerical solutions of the balance equation of beams on elastic basis, using the Finite Element Method and applying the variational methods, i.e., Placement, Sub-regions and Least Squares Method, aiming to compare the results obtained through numerical experiments and the analytical solution, to identify the variational method that provides the best approximate solution, befitting the analytical solution. This is a bibliographic review, with descriptive approach and numerical simulations using the programming language, Phyton. We compared the solutions of the model problem for two different cases, using the methods mentioned above, noting that in the 1st case, the Methods of Sub-regions and Placement provide the best approximation for vertical displacements, with a polynomial base function, while in the 2nd case the trigonometric function provides a better approximation, presenting significant variations in relation to the 1st case, due to changes in parameters, spring coefficient (K), modulus of longitudinal elasticity (E) and cross-sectional inertia (I). Thus, starting from this formulation, other problems frequently encountered in engineering can be analyzed, such as continuous beams and dynamic analysis of beams.