MODELING AND SIMULATION OF FLUID FLOWDYNAMICS FOR CO₂ MIGRATION IN TWO-DIMENSIONAL SALINE AQUIFERS
DOI:
https://doi.org/10.14295/vetor.v34i2.18549Keywords:
finger growth, Saffman-Taylor instability, CO₂ sequestration, CO₂ plume migrationAbstract
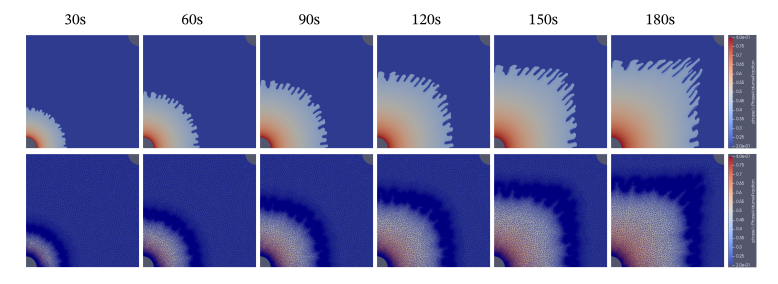
Geological carbon sequestration is increasingly recognized as a promising solution for mitigating CO2 emissions by storing CO2 in geological formations such as saline aquifers. Although recent research has primarily focused on optimizing CO2 trapping mechanisms to enhance storage efficiency, the flow dynamics of CO2 plume migration—particularly the propagation and growth of fingers—remain insufficiently understood. In response to these challenges, we develop a model to simulate CO2 plume migration in both homogeneous and heterogeneous porous media within two-dimensional (2D) saline aquifers. This study utilizes high-order reservoir simulations within the ICFERST framework, employing the control volume finite element method (CVFEM) to specifically capture the viscous instabilities associated with CO2 plume migration. The simulation process integrates various mesh resolutions and incorporates adaptive mesh optimization (AMO). Our results indicate that increasing mesh resolution significantly enhances the ability to accurately capture the formation and growth of CO2 fingers. In homogeneous porous media, AMO effectively balances accuracy and computational efficiency by dynamically refining or coarsening the mesh in critical regions. In heterogeneous porous media, simulations reveal the emergence of wider and larger fingers compared to those observed in homogeneous settings, with bifurcations occurring at locations where relative permeability undergoes significant changes.
Downloads
References
A. Peter, D. Yang, K. I.-I. I. Eshiet, and Y. Sheng, “A review of the studies on CO2 –brine–rock interaction in geological storage process,” Geosciences, vol. 12, no. 4, p. 168, 2022. Available at: https://doi.org/10.3390/geosciences12040168
H. Class, A. Ebigbo, R. Helmig, H. K. Dahle, J. M. Nordbotten, M. A. Celia, P. Audigane, M. Darcis, J. Ennis-King, Y. Fan et al., “A benchmark study on problems related to CO2 storage in geologic formations: summary and discussion of the results,” Computational geosciences, vol. 13, pp. 409–434, 2009. Available at: https://doi.org/10.1007/s10596-009-9146-x
P. G. Saffman and G. I. Taylor, “The penetration of a fluid into a porous medium or hele-shaw cell containing a more viscous liquid,” Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, vol. 245, no. 1242, pp. 312–329, 1958. Available at: https://doi.org/10.1098/rspa.1958.0085
H. P. Langtangen, A. Tveito, and R. Winther, “Instability of Buckley-Leverett flow in a heterogeneous medium,” Transport in Porous Media, vol. 9, no. 3, pp. 165–185, 1992. Available at: https://doi.org/10.1007/BF00611965
J. M. Nordbotten, M. A. Celia, and S. Bachu, “Injection and storage of CO2 in deep saline aquifers: analytical solution for CO2 plume evolution during injection,” Transport in Porous media, vol. 58, pp. 339–360, 2005. Available at: https://doi.org/10.1007/s11242-004-0670-9
V. Vilarrasa, D. Bolster, M. Dentz, S. Olivella, and J. Carrera, “Effects of CO2 compressibility on CO2 storage in deep saline aquifers,” Transport in porous media, vol. 85, pp. 619–639, 2010. Available at: https://doi.org/10.1007/s11242-010-9582-z
J. J. Hidalgo, C. W. MacMinn, and R. Juanes, “Dynamics of convective dissolution from a migrating current of carbon dioxide,” Advances in water resources, vol. 62, pp. 511–519, 2013. Available at: https://doi.org/10.1016/j.advwatres.2013.06.013
S. Pramanik and M. Mishra, “Coupled effect of viscosity and density gradients on fingering instabilities of a miscible slice in porous media,” Physics of Fluids, vol. 28, no. 8, 2016. Available at: https://doi.org/10.1063/1.4961042
M. Norouzi and M. R. Shoghi, “A numerical study on miscible viscous fingering instability in anisotropic porous media,” Physics of Fluids, vol. 26, no. 8, 2014. Available at: https://doi.org/10.1063/1.4891228
A. A. Yazdi and M. Norouzi, “Numerical study of Saffman–Taylor instability in immiscible nonlinear viscoelastic flows,” Rheologica Acta, vol. 57, pp. 575–589, 2018. Available at: https://doi.org/10.1007/s00397-018-1101-0
A. Bonazzi, B. Jha, and F. P. de Barros, “Influence of initial plume shape on miscible porous media flows under density and viscosity contrasts,” Journal of Fluid Mechanics, vol. 972, p. A19, 2023. Available at: https://doi.org/10.1017/jfm.2023.710
A. Pouplard and P. A. Tsai, “Controlling viscous fingering instabilities of complex fluids,” Scientific Reports, vol. 14, no. 1, p. 2338, 2024. Available at: https://doi.org/10.1038/s41598-024-52218-w
K. Christou, W. Radünz, B. Lashore, F. de Oliveira, and J. Gomes, “Numerical investigation of viscous flow instabilities in multiphase heterogeneous porous media,” Advances in Water Resources, vol. 130, pp. 46–65, 2019. Available at: https://doi.org/10.1016/j.advwatres.2018.10.010
NORMS/AMCG. (2024) ICFERST: Imperial College Finite Element Reservoir Simulator. Available at: http://multifluids.github.io/
C. J. Cotter, D. A. Ham, C. C. Pain, and S. Reich, “LBB stability of a mixed galerkin finite element pair for fluid flow simulations,” Journal of Computational Physics, vol. 228, no. 2, pp. 336–348, 2009. Available at: https://doi.org/10.1016/j.jcp.2008.09.014
M. D. Jackson, J. R. Percival, P. Mostaghimi, B. S. Tollit, D. Pavlidis, C. C. Pain, J. L. Gomes, A. H. El-Sheikh, P. Salinas, A. H. Muggeridge et al., “Reservoir modeling for flow simulation by use of surfaces, adaptive unstructured meshes, and an overlapping-control-volume finite-element method,” SPE Reservoir Evaluation & Engineering, vol. 18, no. 02, pp. 115–132, 2015. Available at: https://doi.org/10.2118/163633-PA
S. Geiger, S. Roberts, S. K. Matthäi, C. Zoppou, and A. Burri, “Combining finite element and finite volume methods for efficient multiphase flow simulations in highly heterogeneous and structurally complex geologic media,” Geofluids, vol. 4, no. 4, pp. 284–299, 2004. Available at: https://doi.org/10.1111/j.1468-8123.2004.00093.x
CoolProp. (2024) CoolProp. Available at: http://www.coolprop.org/
I. H. Bell, J. Wronski, S. Quoilin, and V. Lemort, “Pure and pseudo-pure fluid thermophysical property evaluation and the open-source thermophysical property library coolprop,” Industrial & Engineering Chemistry Research, vol. 53, no. 6, pp. 2498–2508, 2014. Available at: http://pubs.acs.org/doi/abs/10.1021/ie4033999
R. Span and W. Wagner, “A new equation of state for carbon dioxide covering the fluid region from the triple-point temperature to 1100 K at pressures up to 800 MPa,” Journal of physical and chemical reference data, vol. 25, no. 6, pp. 1509–1596, 1996. Available at: https://doi.org/10.1063/1.555991
A. Laesecke and C. D. Muzny, “Reference correlation for the viscosity of carbon dioxide,” Journal of physical and chemical reference data, vol. 46, no. 1, 2017. Available at: https://doi.org/10.1063/1.4977429
W. Wagner and A. Pruß, “The IAPWS formulation 1995 for the thermodynamic properties of ordinary water substance for general and scientific use,” Journal of physical and chemical reference data, vol. 31, no. 2, pp. 387–535, 2002. Available at: https://doi.org/10.1063/1.1461829
M. L. Huber, R. A. Perkins, A. Laesecke, D. G. Friend, J. V. Sengers, M. J. Assael, I. N. Metaxa, E. Vogel, R. Mareš, and K. Miyagawa, “New international formulation for the viscosity of H2 O,” Journal of Physical and Chemical Reference Data, vol. 38, no. 2, pp. 101–125, 2009. Available at: https://doi.org/10.1063/1.3088050
G. Andersen, A. Probst, L. Murray, and S. Butler, “An accurate PVT model for geothermal fluids as represented by H2 O-CO2 -NaCl mixtures,” in University of North Texas Libraries, UNT Digital Library. UNT Libraries Government Documents Department, 1992. Available at: https://digital.library.unt.edu/ark:/67531/metadc885359/m1/1/
S. Mao and Z. Duan, “The viscosity of aqueous alkali-chloride solutions up to 623 K, 1,000 bar, and high ionic strength,” International Journal of Thermophysics, vol. 30, pp. 1510–1523, 2009. Available at: https://doi.org/10.1007/s10765-009-0646-7
R. H. Brooks and A. T. Corey, Hydraulic Properties of Porous Media, ser. Hydrology Papers ; no. 3. Fort Collins, CO: Colorado State University, Hydrology and Water Resources Program, 1964. Available at: https://www.proquest.com/books/hydraulic-properties-porous-media-r-h-brooks-t/docview/47928924/se-2?accountid=8155