Influence of information criteria choice on the proportion of non-rejection of the null hypothesis of the ADF test considering the presence of unit roots
DOI:
https://doi.org/10.14295/vetor.v33i2.15163Keywords:
Unit root test, Information Criteria, ADFAbstract
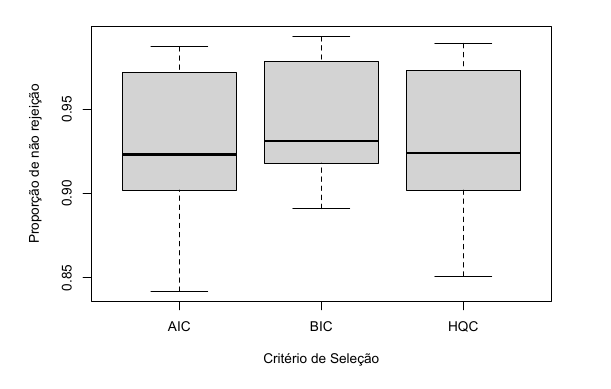
One of the various techniques used for time series analysis is econometric analysis, where in many cases it is necessary to verify the stationarity of the series. A non-stationary series presents the presence of unit roots, which makes it unsuitable for making forecasts. In this context, the so-called unit root tests have emerged, among which the Augmented Dickey-Fuller (ADF) test stands out. One of the crucial steps in applying the ADF test is the selection of lags. To select the lags to be applied in the test, it is necessary to define a maximum number from which the ideal number to be used in the ADF application will be selected. This ideal number can be determined with the aid of information criteria, such as the traditional AIC, BIC, and HQC. This study evaluated the influence of the choice of information criteria on the test result, considering the presence of unit roots. After the construction of scenarios, application of tests, and analysis of variance, no evidence was found that the choice of information criteria can interfere with the rate of non-rejection of the null hypothesis in the ADF test.
Downloads
References
F. M. Bayer e A. M. Souza, “Wavelets e modelos tradicionais de previsão: Um estudo comparativo,” Revista Brasileira de Biometria, vol. 28, no. 2, pp. 40–61, 2010. Disponível em: http://jaguar.fcav.unesp.br/RME/fasciculos/v28/v28_n2/A3_Fabio_Adriano.pdf
D. N. Gujarati e D. C. Porter, Econometria básica-5. Amgh Editora, 2011.
S. E. Said e D. A. Dickey, “Testing for unit roots in autoregressive-moving average models of unknown order,” Biometrika, vol. 71, no. 3, pp. 599–607, 1984. Disponível em: https://doi.org/10.1093/biomet/71.3.599
A. Silveira, V. Mattos, L. Nakamura, M. Amaral, A. Konrath, e A. Bornia, “Análise do valor-p determinado pela estatística na aplicação do teste de dickey-fuller aumentado,” Trends in Computational and Applied Mathematics, vol. 23, pp. 283–298, 2022. Disponível em: https://doi.org/10.5540/tcam.2022.023.02.00283
H. Akaike, “Maximum likelihood identification of gaussian autoregressive moving average models,” Biometrika, vol. 60, no. 2, pp. 255–265, 1973. Disponível em: https://doi.org/10.1093/biomet/60.2.255
G. Schwarz, “Estimating the dimension of a model,” The Annals of Statistics, pp. 461–464, 1978. Disponível em: https://www.jstor.org/stable/2958889
E. J. Hannan e B. G. Quinn, “The determination of the order of an autoregression,” Journal of the Royal Statistical Society: Series B (Methodological), vol. 41, no. 2, pp. 190–195, 1979. Disponível em: https://doi.org/10.1111/j.2517-6161.1979.tb01072.x
D. A. Dickey e W. A. Fuller, “Distribution of the estimators for autoregressive time series with a unit root,” Journal of the American Statistical Association, vol. 74, no. 366a, pp. 427–431, 1979. Disponível em: https://doi.org/10.1080/01621459.1979.10482531
R. L. S. Bueno, Econometria de séries temporais. Cengage Learning, 2018.
G. W. Schwert, “Why does stock market volatility change over time?” The Journal of Finance, vol. 44, no. 5, pp. 1115–1153, 1989. Disponível em: https://doi.org/10.1111/j.1540-6261.1989.tb02647.x
T. L. Sobral e G. Barreto, “Utilização dos critérios de informação na seleção de modelos de regressão linear,” Proceeding Series of the Brazilian Society of Computational and Applied Mathematics, vol. 4, no. 1, 2016. Disponível em: https://proceedings.sbmac.org.br/sbmac/article/download/1144/1157
R. D. C. Team, “A language and environment for statistical computing,” http://www. R-project. org, 2009.
A. Zeileis e T. Hothorn, “Diagnostic checking in regression relationships,” R News, vol. 2, no. 3, pp. 7–10,
Disponível em: https://journal.r-project.org/articles/RN-2002-018/RN-2002-018.pdf
H. Levene, “Robust tests for equality of variances,” Contributions to probability and statistics, pp. 278–292, 1960. Disponível em: https://doi.org/10.2307/2285659
A. Hall, “Testing for a unit root in time series with pretest data-based model selection,” Journal of Business & Economic Statistics, vol. 12, no. 4, pp. 461–470, 1994. Disponível em: https://www.tandfonline.com/doi/abs/10.1080/07350015.1994.10524568